Long Division - How to Conquer this Method
- Joanne Adams
- Feb 4, 2023
- 5 min read
Updated: Oct 28, 2024
This is definitely a 'Marmite Method'. Some children love it and some children hate it. It's often the method parents mention to me that they struggled with at school and have never used since. Calculators, now available on mobile phones, are often the 'go-to' method for adults today. However, children in primary schools need to be able to have a wealth of mental and written methods in order to calculate a variety of different arithmetic questions, without the use of a calculator. They also need to be proficient in these methods to solve questions in a variety of contexts, referred to as 'Reasoning' in the curriculum.

Just like any other written method in maths, children need to have the right foundations in place before learning this method. Can they confidently use the Bus Stop method with their times tables facts? Do they have a good knowledge of place value and recognise multiplication facts as division facts too? The children who have the most success with this method understand why it works rather than following a series of memorised steps. The Primary National Curriculum stresses the importance of teaching for understanding.
Many people see the Long Division method as tricky. Let's break this method down into a series of steps and work out how and why it works.
The first thing that we need to understand is that Long Division is a method of dividing each digit (value) within the question, one step at time. The calculation relies on the understanding that we are dividing a quantity of thousands, then hundreds, then tens and finally ones into groups of a particular number. We call this the divisor (the number written on the left of the calculation: the number we are dividing by). I use colour in my demonstrations to make it easier to see the steps that are worked through.
The Long Division method can be used for dividing by single digits but I tend to reserve it for the division of larger numbers by a two digit divisor. Long Division requires a logical approach and neat recordings as you work through the stages of the question. I strongly recommend the use of squared paper to support the recording of this method. Children often benefit from creating a little fact file for the divisor too. (I demonstrated an example of a Fact File in a previous blog about the Chunking method of division).
Lets use the following question to explore how to use this method:
Question
6510 divided by 23?
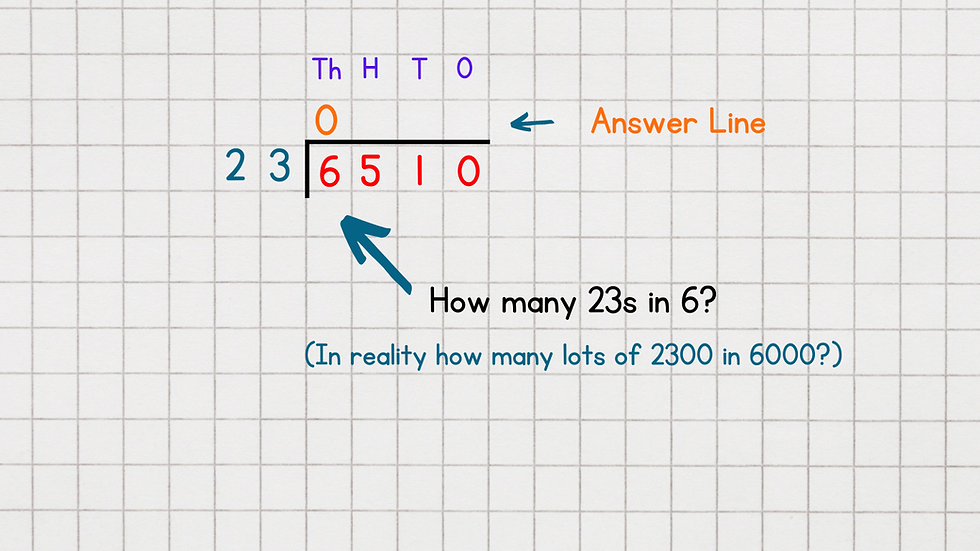
Step One (Thousands):
a) The calculation begins by asking the question, "How many lots of 23000 are there in 6000?" This question is too big for most of us to process and therefore you will hear the simplified question that relies on place value:
Q: How many 23s are there in 6?
A: 0
When framed this way, the obvious answer is zero. This answer 0 is placed in the first column on the answer line, at the top of the calculation. This shows that there are no lots of a thousand in the answer.
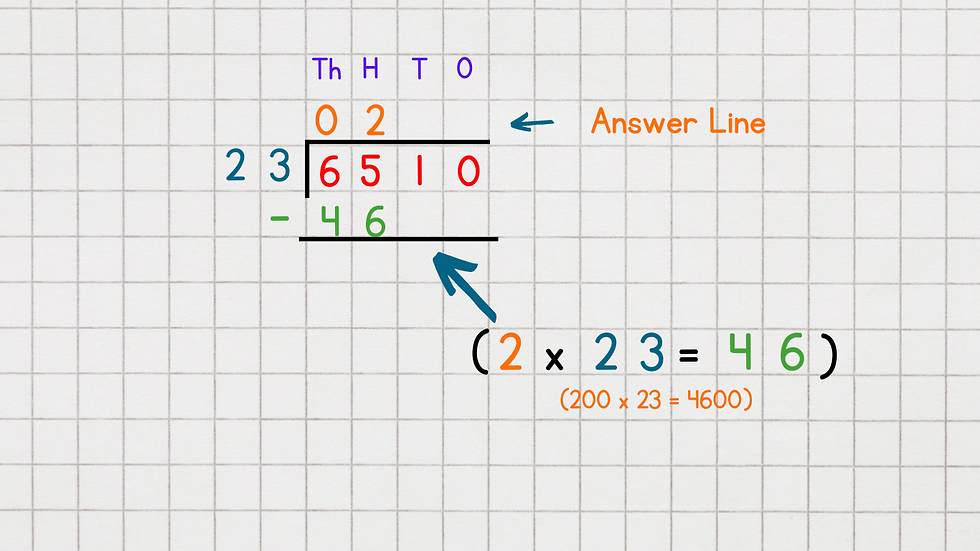
Step Two (Hundreds)
a) The next step is to move along the calculation to add in the next value, "How many lots of 2300 are there in 6500?" Again we can simplify this question using place value into:
Q: How many 23s are in 65?
A: 2
To answer this question we need to think in terms of multiples of 23. Two lots of 23 is 46. Therefore we write the 2 on the answer line at the top. We write 46 at the bottom of the calculation ready to subtract it so that we know what we are left with.
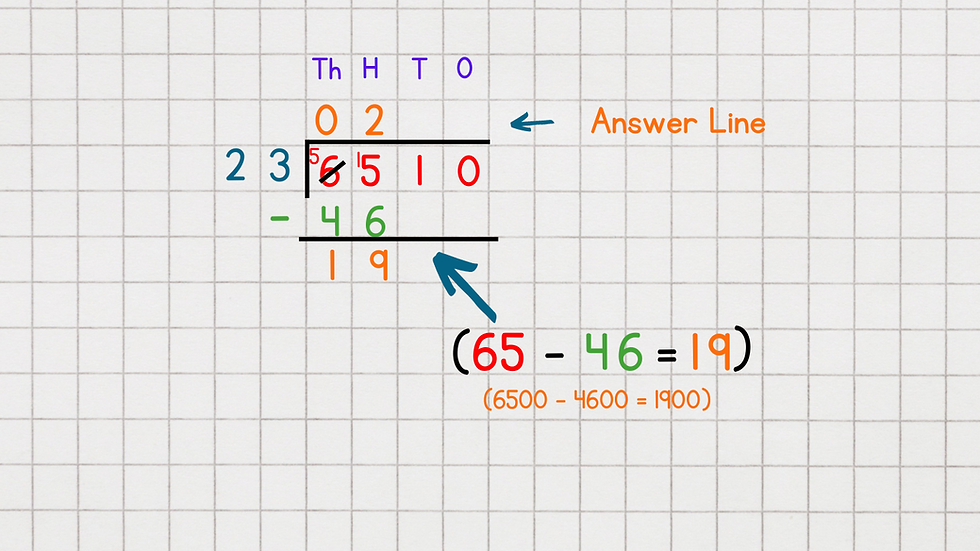
b) The next step is to subtract the 46 to see what you have left to work with.
65 - 46 = 19
19 is written at the bottom of the calculation ready for the next step (Remember: 19 is really 1900 but working in columns ensures that all the place value is done for us).
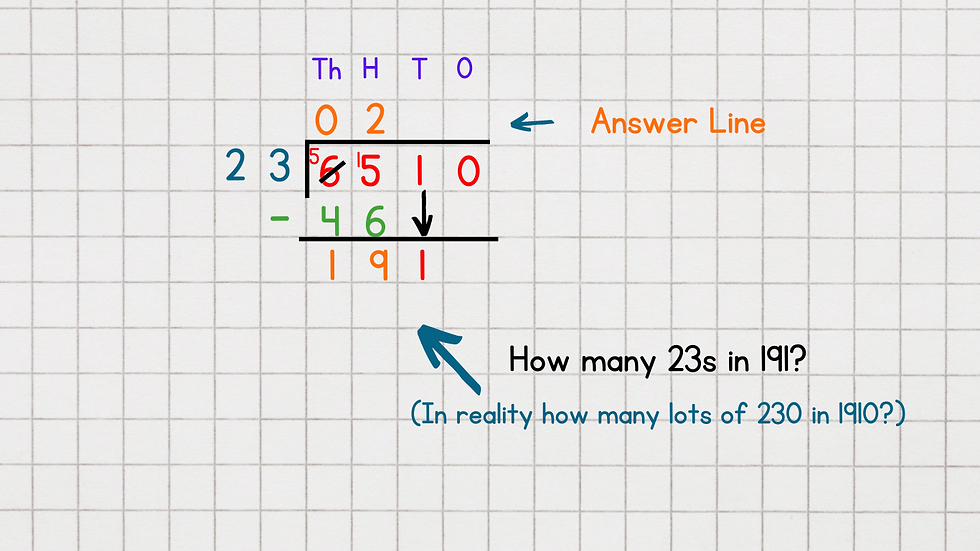
Step Three (Tens)
a) We are now ready to bring down the 1 from the 'Tens' column. This creates the number 191 (simplified).
b) The next question is:
Q: How many 23s in 191?
We know that 23 x 10 = 230 (too big). We know that 23 x 2 = 46. Therefore: 230 - 46 = 184.
(10 lots - 2 lots = 8 lots)
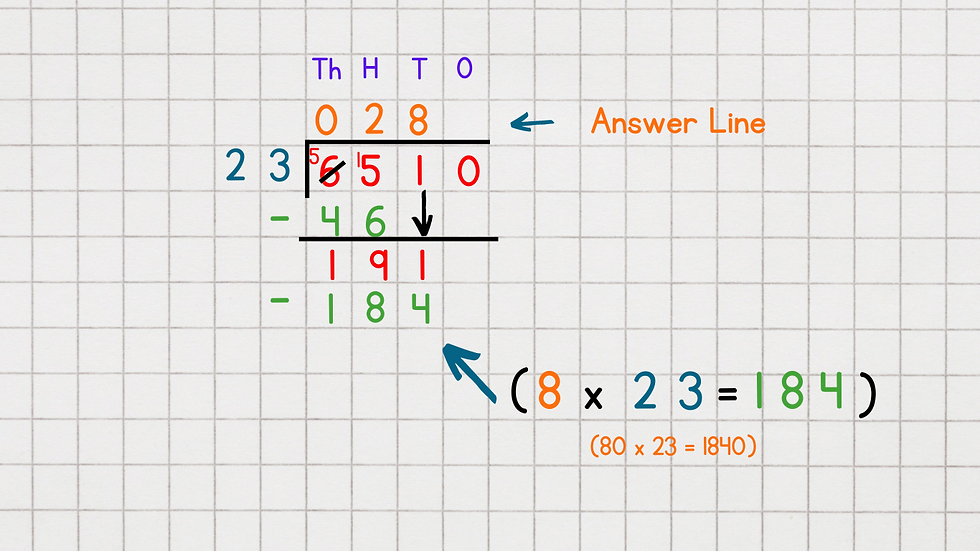
A: 8 x 23 = 184
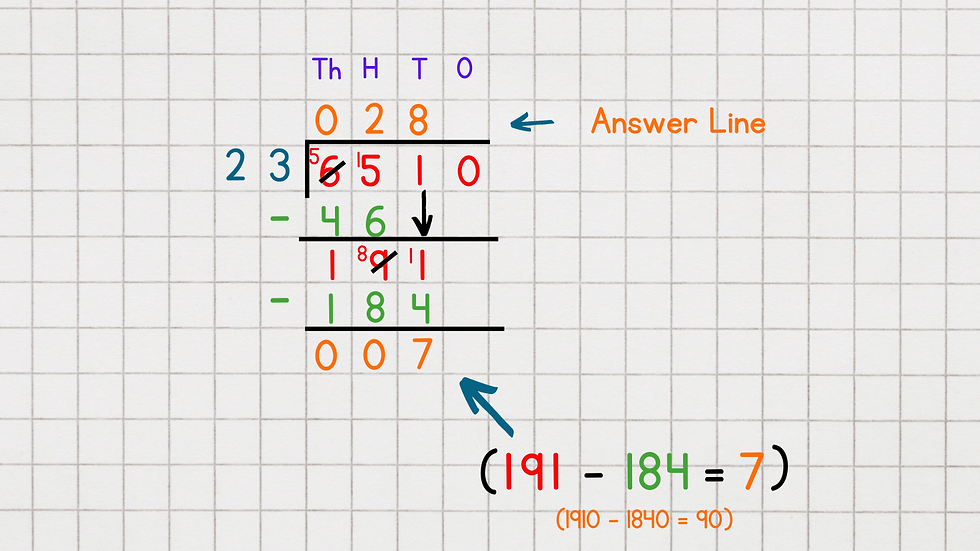
c) The 8 goes on the answer line at the top, in the 'Tens' column and the 184 goes at the bottom of the calculation ready to subtract.
Q: 191 - 184 = 7
We are now left with just 7 lots of 'Ten' .
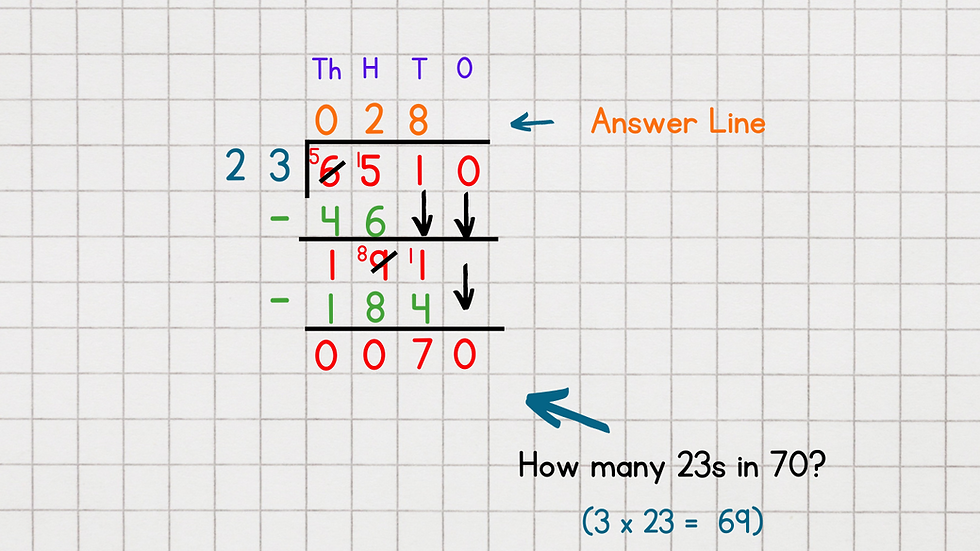
Step Four (Ones)
a) For the last step, bring down the final digit '0' in the 'Ones' column. There is now just 70 left to divide.
b) The last part of the calculation asks:
Q: How many 23s in 70?
A: 3 x 23 = 69
The 3 goes on the top answer line and the 69 goes at the bottom of the calculation.
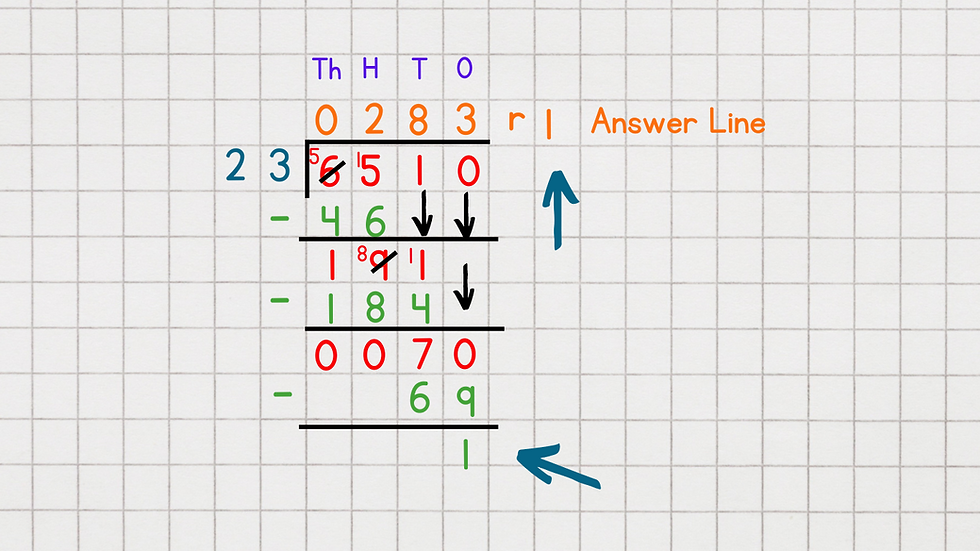
c) To complete the calculation you need to subtract 69 to identify if there are any remainders:
Q: 70 - 69 = 1
Question
6510 divided by 23 = 283 remainder 1
From my demonstration above, I think I have sadly proved why children find it so tricky but when practised, this method becomes second nature. You may have noticed that the series of steps is just repeated with each value as you move across the question.
Primary Schools don't usually teach this method until the last few years of Key Stage 2. Children need a secure knowledge of place value, their times tables and the ability to recognise multiples of ten and 100 of these facts before they can make use of this method confidently.
For some children, this is not a method that works for them. They prefer to stick to the Bus Stop method and learn to write it in a more spaced out way. The Primary National Curriculum encourages children to be taught a variety of different calculation methods and adopt the ones that they feel most comfortable with, a method that they can apply in a variety of contexts. Mathematics is not a linear subject. The art of complex maths is to be able to look at one problem and deconstruct into a series of calculations. There is often a variety of different approaches to solve one problem and we don't all think in the same way.
If your child doesn't master Long Division, it's not the end of the world and it won't halt their progress in maths, they just need to ensure they can use the Bus Stop Method accurately.
For more information about the methods and strategies children learn in Primary School, join my FREE Facebook Group: Primary Parents' Group









Comments